Left Leaning Red Black Tree Implementation in AS3

One of the most interesting Data Structure out there is probably Tree. As the name may suggest, it’s about arranging item keeping in mind the typical tree shape ( reversed with the root on top,leafs on buttom).

In this blog post i’ll try to cover the basic aspects of Trees, proposing a new implementation of the Red-Black Tree.

If you arrived here, you probably know what a Red Black tree is, and why is an interesting data structure, just to refresh a little bit here following a quick overview:

Requirements (invariants)

1) A node is either red or black.
2) The root is black.
3) All leaves are black.
4) Both children of every red node are black.
5) Every simple path from a given node to any of its descendant leaves contains the same number of black nodes.

These introduced constraints against the less bounded binary search trees, let the Red-Black tree longest path from the root to any leaf beeing no more than twice as long as the shortest path from the root to any other leaf in that tree (balanced). This result in algorithm cost of search tend to O(log(n)). The downside is the insertion and delete cost of O(log(n)) too. I must say that is still a fair trade.
The real downside of RB tree is the complexity of the algorithm behind it, that is hard to implement. Usually languages have they own basic implementation of data structures (major languages at least), if not already implemented there are some problems:

– books usually hide part of the implementation (sometimes they just skip and leave the hard work to the reader, since it’s an high risk task this is not a good idea)

– remove and insertion must provide the Recostruction and Coloration,that are the fixup process, to keep the Tree in the right form. In the original structure draft by Rudolf Bayer in 1972 wasn’t specified the effective implementation of the delete operation, so through years there was many implementation, usually with many lines of code, and different approaches.

Before getting into the new RB implementation i must add some explanation about language related issues.

AS3 hasn’t any generics way to handle data.

Generics is the ability to specify a type that will be used within a class without explicitly defining the type. Generics is the way this practice is know in Java world, for oldschool C++ the keyword is Template. In general writing code using generics let you manage one data structure for different type of objects without knowing exactly with object type will be later used.

(there is an interesting article on why as3 needs generics here)

This means that we are unable to implement a general solution (read data structure), but we should typed and force typing just to get better performance (if you are thinking to handler generics object, believe me it’s a bad idea – dynamic type checking is always a bad idea on semi-compiled languages).
So main point is to custom the generic code i wrote (and attach at the end of the blog entry) customizing to your specific purpose. (just search for the “object” and replace with your “type”.

AS3 hasn’t any ready to use implementation of the comparable concept.

This is not only a language lack, it’s about also the way developer think to the question.
Main problem is that data structures usually deals with object, in doing this algorithms (search, order, insertion) take advance of the fact that object are comparable between each other.
In java this concept is well implemented/exposed by the overridable method compares and the comparables interface.
Unfortunatly again this is not a best practice used in the AS3 words.
Let say, that dealing with data structure will force you to find a way to represent the concept that object are comparable and how to take a decision about the fact that A comes from B and not viceversa.

AS3 hasn’t the concept of overloading method.

This is slightly different from set default value to function formal values.
The lack of overloading usually leads to an higher branches complexity (if-then-else levels).
In my implementation i prefered to split overloaded methods into different methods instead of collapsing into one method with higher branches complexity.

So when you’ll download the implementation at the end of this blog post remember to:

1) strictly defined the type of values that LLRB tree handles (now is set to object, just search and replace it)
2) choose a way to compare objects (actually i’m use int as keys, so you can easily define that keys A < B < C, at this point Collision is not handled, if you try to insert object with key B again into the tree, this simply override the B-object already in)
3) be good with my implementation, in java would look much elegant, but as3 as some limits i must workarounded.

What is a LLRB Tree

Finally straight to the point.
In September 2008 (surprised for the recent date ?! ) Robert Sedgewick (a pillar in Computer Science panorama) proposed for the first time the Left leaning tecnique to color the Red Black Tree, introducing additional invariant that all red links must lean left except during inserts and deletes.

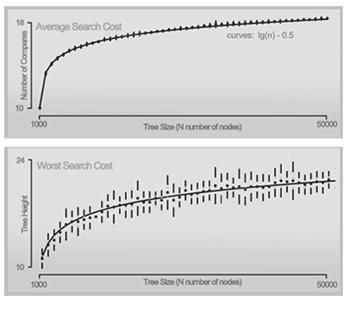
What may look like a “simply” modification leads to great results:
– A random successful search examines lg(N) – 0.5 nodes. While the normal RB has a worst case where the search takes C * lg(N) where C is a constant > 1.
– The average size of left subtree exhibits log-oscillating behavior in growing tree
– Experimental studies have not been able to distinguish these algorithms from optimal.
– Simplify the isomorphism from 2-3 and 2-3-4 tree: the left- leaning versions of 2-3 trees and top-down 2-3-4 trees differ in the position of one line of code.
– Simple implementation (that’s true for me at least. Just 250 loc for the entire data structure and 120 for the core only, while a normal RB tree request around 400 for the core only.

Here the classes:

LLRB DataStruct (2.9kb)

Here a firestarter piece of code:

// CREATE A TREE
var tree:LLRBTree = new LLRBTree();
// ADD AN OBJECT
tree.put(key,object);
// SEARCH FOR AN OBJECT
tree.find(key);

// REMOVE AN OJBECT, returns the object removed
tree.remove(key);

// OTHER INTERESTING METHOD
tree.deleteMax(); // find and remove the higher element
tree.deleteMin(); // find and remove the lower element
tree.max(); // find the higher element
tree.min(); // find the lower element
tree.height() // the height of the tree.

Here a not so much interesting benchmark about time elapse in serching ordered data structures with a binary search (for array and vector) and llrb tree search. (Not a fan of this kind of benchmark, but ppl enjoy it, so here you are.)