
As programmers we are used to deal with numbers every day.
We feel good with math, since there are no shading, and any assertion can be only true or false.
What we usually don’t know is that computers make errors. They do it lots of time, even on basic calculation,where every an human usually dosn’t. Knowing this will let us handling the sad problem.
Even if ActionScript 3 offers us only 3 basic data Types (int, uint and Number) that is , compared with other Languages really a small number, we still suffer the same problem, since is not a language problem, but simply how computers rappresents numbers.
The Floating Point rappresentation.
In Math we usually work with Real numbers (the R set) that are an infinite set of number, where number can have an infinite number of digits (basicly periodical and irrational). Let’s think to PI or the result of fraction like 1/3 to image fews.
Good exemple to get this idea is to think to a number, than divide by 2, and iterate this: I challange you finding an end to this.
A calculator has a limited number of significant digit, that let us figuring out that we can’t rappresent every number in R.
There are also some “minor” problem on how a number is rappresentend inside a calculator, that is the base: we count in base 10 (we have 10 fingers we can count on, in past other base was picked like 60 and 12, both smarter than base 10, due to the bigger number of natural divisor of the base), calculators work in base 2 (since the electronic behind easily works with 2-state voltage condition).
Both the above reason lead to the floating point rappresentation, that even if is not the only existing rappresentation is the most used. (Other two major rappresentions are Fixed point and integer).
The advantage of floating point rappresentation over others, are the wider range of values it can rappresent.
Since the concept of Floating point was formulated first time, many standards was proposed, IEEE decided to make their own standard set of rules for what was recorded in 2008 as IEEE 754 FP rappresentation scheme.
The idea is to use 4 main format, based on the avaiable bit (note: i’m not used to make plural of words like “bit” ), that are 16 (Half), 32 (Single), 64 (Double), 128 (Quadruple).
The avaiable bit are divided into 3 groups: Sign, Exponent, Significant. First group “Sign” is composed by one bit only, 0 if the number is positive, 1 if negative. Exponent group contains 8 bit of the 32 in Single format and 11 bit of the 64 in double format. Exponent (in the 8bit case) can assume 256 different values (2^8): 0 and 255 are reserved number, while the other values rappresent number between -126 and 127 (a tecnical note: this process is called polarization of the number and don’t request a bit as sign, they just move the interval from 0-254 to -126 and 127 in the decoding phase)

The bit left (23 in the single rappresentation and 52 on the 64 bit rappresentation) are used for the Significant group. It rappresents, as name can suggest, the significant digits of the number normalized. This number is also called “mantissa”. The process of normalization is needed for avoiding different rappresentation of the same number.
For exemple the number 30 can be write as 3*10^3, or as 300*10^-1, forcing the normalizationis the only way to know that 30 can be rappresented in Fp only as 0.3 * 10^2.
So now we have all our parts to star moving our “real life” number into floating point rappresentation.
A general number can be rappresented as fl(x) = sgn(x)(0.a1a2…an)b^p
The Problems with FP.
We said that we have a limited number of bits. this automaticly set an upper bount to our desire of mapping real world number into a calculator. Without any standard rappresentation we can easily know that n bit can rappresent up to 2^n-1 number (where any number is +1 from the previous).
Living in the “integer” world is not so cool, and soon we need our point.
This is where floating point world start.
On 64bit double precision, upper bound is 1.79769313486231e+308 that is the result of a all-1 mantissa and the maximum exponent.Lower bound (in the absolute meaning, so the closest number to 0) is 4.9406564584124654e-324.
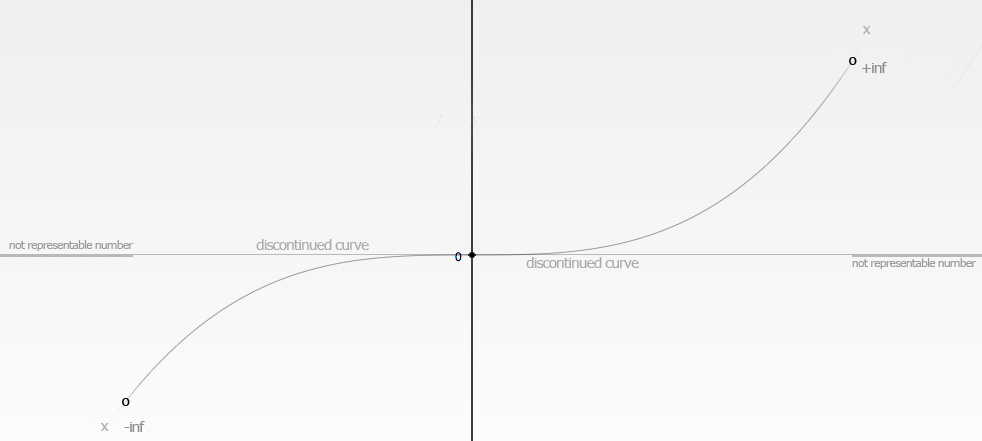
As you can see in this image, the upperbound is marked both on the Minus and on the Plus side, the next value major than the Upperbound is marked as Infinity (+inf and -inf). This is a marked set of bit that floating point notation use for keep consist some operation (like multiply a number for infinity resulting in infinity)
What really metter is the distribution of number rappresented by the curve, and the hole between any floating point number in that.
This is also called FP relative accuracy where “Accuracy” refers to how close a measurement is to the true value.
Just run the following as3 code.
var e = 1;
var k = 0;
while((e+1) > 1){
e /= 2;
k++;
}
trace(e *= 2,k);
trace( "The number 1: ", 1);
trace( "The closer smaller number to 1: ", 1+e);
trace( "The useless addition; ", 1+e/2);
We actually found the closest number to 1, and we also proof that any try to add number minor than this number is useless.
This magic number is called EPS, and rappresent the space between two close FP number. Any number between don’t exist in calculator.
We are facing precision loss of the result.
This affect all the basic operation, and some property we normaly use are not longer valid.
Associative property is not valid in FP:
(x+y)+z != x+(y+z)
(x*y)*z != x*(y*z)
(ie x = −2^100, y = 2^100, and z = 1.)
Distributive propery is not valid in FP:
x*(y+z) != (x*y)+(x*z)
(ie x = 0.5, y = largest possible number, and z = 1)
Simmetry is not valid in FP:
x*y != y*x
(ie x = 0.4 , y=0.3)
Conclusion
Working with Floating Point operations can be legal in principle, but the result can be impossible to represent in the specified format, because the exponent is too large or too small to encode in the exponent field. Such an event is called an overflow (exponent too large), underflow (exponent too small) or denormalization (precision loss).